New Tech Report: Efficient and Precise Typestate Analysis by Determining Continuation-Equivalent States
Eric | September 10, 2009
I just uploaded a new Technical Report. The report (currently under submission) describes a novel typestate analysis, called Nop-Shadows Analysis, that I implemented for my doctoral dissertation. The analysis is certainly one of my dissertation’s major technical contributions. I implemented the Nop-Shadows Analysis in the Clara framework, which means that you are welcome to download it, try it out or extend it.
Continuation-equivalent states
So what are these continuation-equivalent states that appear in the title? We say that two automaton states s1 and s2 are continuation-equivalent if, given the current code location and all possible continuations of the execution after this location we either will or won’t reach a violating typestate regardless of whether we are in s1 or s2. Maybe an example is in order… (taken from the paper)
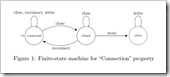
Assume that we want to evaluate the “ConnectionClosed” property that is depicted by the state machine on the right. The property says that it is an error to write to a closed Connection (where connections can alternate between an “connected” and a “closed” state through “close” and “reconnect” operations. Next, assume that we want to statically evaluate this property on the following simple program…
The figure on the right shows a program that is annotated with the analysis information that the Nop-Shadows Analysis computes. The example program violates the connection property by closing the connection (even twice, at lines 5 and 6), and then writing to the connection (line 7). Note, though, that all other statements in this program are irrelevant to the property violation. In particular, one does not need to monitor the “close” and “reconnect” operations at lines 3 and 4 because they precede the violating fragment of the run. Conversely, the operations at lines 8 to 10 follow this fragment, and hence do not need to be monitored either. A little more subtle, even of the the two“close” events at lines 5 and 6, it is correct to omit monitoring one of them. (But not
both!) The static analysis that we present in the paper will eliminate the instrumentation at exactly those shadows that we just identified as irrelevant—“nop shadows”, as we call them. Instrumentation will only remain in lines 5 and 7, or 6 and 7—an optimal result for this program.
The Nop-Shadow Analysis uses a deterministic finite-state machines for the mirror language of the original automaton’s language (see Figure 4b) to construct for every statement a partitioning of automaton states. States that are in the same class of the partition are continuation-equivalent. For instance, at line 3, which transitions from state 0 to 1, states {0,1,2} are all continuation-equivalent. Therefore there is no need to monitor the transition at this line – the transition is irrelevant!
Results
The analysis has several nice properties. Firstly, it is relatively efficient, and it is precise (see Figure). Also, it seems to be the first analysis of its kind (a flow-sensitive typestate analysis generating residual runtime monitors) that is sound. Unfortunately, we found an unsoundness problem in two analyses that we and others published earlier. The paper describes this problem in the related-work section. For my dissertation, I proved the novel Nop-Shadows Analysis sound, which was relatively easy because the analysis follows a relatively simple design.
Related Posts
No related posts.
